에지 검출 : 물체 내부는 명암이 서서히 변하고 물체 경계는 명암이 급격히 변하는 특성 활용
- 미분 : 변수 x가 미세하게 증가했을 때 함수 변화량을 측정하는 기법
- 정수 좌표를 쓰는 디지털 영상에서는 x의 최소 변화량이 1이기에, δx =1 로 한다

디지털 영상의 미분

- 해당 식을 영상 f에 적용하는 일은 필터 u(에지 연산자)로 컨볼루션 하여 구현.
- 필터 u의 중심점은 왼쪽 화소임.
- 에지영상 f’은 명암값이 커지면 미분값으로 양수를, 작아지면 음수를 갖는다.

[현실 세계의 램프 에지] : 명암이 몇 화소에 걸쳐 변하는 에지
- 에지의 두께가 1보다 큰 경우, 에지의 정확한 위치를 찾는 데에 문제가 생김.
- 1차 미분은 에지 발생 여부, 에지가 어떤 방향을 향하는지에 대한 정보가 제공됨.
- 2차 미분 영상 f’’은 컨볼루션을 두 번 적용하여 얻을 수 있지만 아래 식을 통해 필터를 설정하면 한 번의 컨볼루션으로 구할 수 있다.


[램프 에지에서 발생하는 봉우리와 영교차]
- 1차 미분 영상 : 에지에서 봉우리 발생
- 2차 미분 영상 : 영교차 발생
- 영교차 : 왼쪽과 오른쪽 부호가 다른 반응이 나타나고 자신은 0을 갖는 위치
→ 1차 미분에서 에지 검출은 봉우리를 찾는 것.
→ 2차 미분 영상에서 에지 검출은 영교차를 찾는 것
1차 미분에 기반한 에지 연산자
- (-1,1)은 너무 작고 대칭이 아니기에 실제로는 (-1, 0, 1)로 확장하여 주로 사용
- 필터를 확장하면 잡음을 흡수하여 더 좋은 성능을 보임.
- 소벨 연산자
: 보다 가까운 상하좌우 화소에 가중치 2를 줌으로써, 에지를 더 뚜렷하게 만드는 필터
- 프레윗 연산자

- 에지 강도 :

- 그레이디언트 방향 :
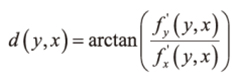
- (f’x와 f’y는 프레윗의 x,y커널 또는 소벨의 x,y커널을 적용한 값
- 에지 방향은 그레이디언트 방향을 90(시계방향)도 회전한 방향으로 정의함.
- 에지 강도 :

[ 소벨 연산자 적용 사례]
- 파란색 화살표는 값을 보고 알게 되는 방향이 아닌 알려준 값.
- f’x, f’y : 소벨 연산자의 X, Y커널을 적용한 값
- 에지강도 : 에지의 뚜렷함을 판단하는데 사용하는 값
- 그레이디언트 방향 : 좌상단이(0,0)으로, 각도가 음수일 때 화살표는 오른쪽과 위쪽 방향을 가리킴. (반시계방향)
- 에지 방향 : 그레이디언트 방향을 90도 회전한 방향
캐니의 목적함수 정의 기준 : 최소 오류율, 위치 정확도, 한 두께
- 얇은 에지일수록 더 잘 정의된 에지!
- 얇은 에지는 이미지에서 변화가 급격한 지점을 나타냄. 따라서 해당 지점에서 에지가 더 정확하게 감지된다.
- 얇은 에지는 이미지에서 더 정확한 위치를 나타낸다.
- 에지가 두꺼워질수록 에지의 위치가 모호해지며 에지의 실제 위치가 어디인지 파악하기 어려워진다.

[ 한 두께 에지를 출력하기 위해 비최대 억제 적용.]
비최대 억제 : 에지 화소에 적용. 에지 방향에 수직인 두 이웃 화소의 에지 강도가 자신보다 작으면 에시로 살아남고 그렇지 않으면 에지가 아닌 화소로 바뀐다.
- 두 이웃 화소와 비교해 자신이 최대가 아니면 억제됨. 지역 최대(극점)만 남기는 전략
- 거짓 긍정 : 실제 에지가 아닌데 에지로 검출된 화소.
- 캐니의 알고리즘은 거짓 긍정을 줄이기 위해 2개의 이력 임곗값 T’low, T’high를 이용한 에지 추적을 추가로 적용.
- 에지 추적은 에지 강도가 T’high이상인 에지 화소에서 시작함. (실제 에지 가능성이 높은 곳에서 추적을 시작하겠다는 의도.)
- 시작 화소가 정해지면 이후 추적은 T’low 임곗값을 넘는 에지를 대상으로 진행
→추적 이력이 있는 이웃을 가진 화소는 에지 강도가 낮더라도 실제 에지로 인정하는 전략. - 캐니는 T’high를 T’low의 2~3배로 설정할 것을 권고함
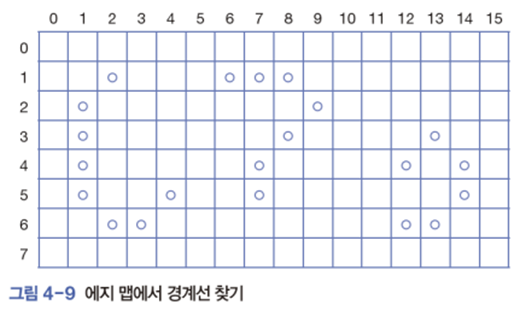
[ 에지 맵에서 경계선 3개를 찾아 연속된 점의 리스트로 표현한 사례]
- 8 – 연결 에지 화소를 서로 연결해 경계선 구성할 수 있음
허프 변환 : 끊긴 에지를 모아 직선 또는 원 등을 검출
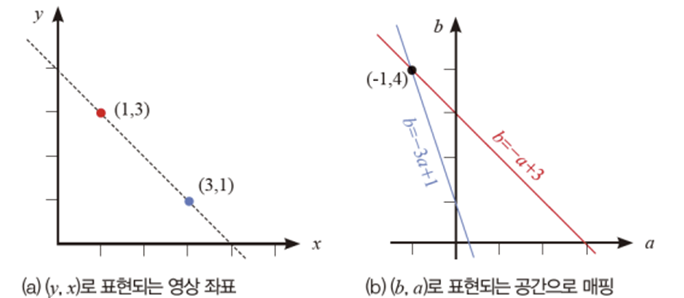
(a) : (x,y)를 지나는 직선은 y=ax+b로 표현할 수 있음. 이를 이용해 두 방정식 세우면
(b) : 두 직선을 가진 새로운 공간(a, b)형성. 두 직선이 만나는 점은 원래 공간에서 두 점을 지나는 직선의 기울기와 y절편이다. (기울기, y절편)
- 두 직선이 만나는 점은 투표로 알아냄. → 2표를 받는 곳
( 각각의 직선은 자신이 지나는 점에 1만큼을 투표.)
#문제점 1#
위의 허프 변환은 이상적인 상황으로, 현실에서는 많은 점들이 있고 이 점들이 일직선을 이루지 못하는 차이점이 있음. 이 문제는 (b, a)공간을 이산화 하고 누적 배열을 만들어 해결한다.
- ex. a와 b의와b의 범위를 -1000~1000으로 설정하고 각각을 크기가 20인 구간 50개로 나누어 칸이 50*50=2500인 2차원 누적배열 v를 만든다. v를 0으로 초기화한 다음 각각의 직선은 자신이 지나는 모든 칸에1 만큼씩 투표한다.
*다수 표를 얻은 점을 결정할 때 비최대 억제 적용하여 지역 최대점 찾음.
#문제점 2#허프 변환은 어떤 선분이 있는지 모르기 때문에 모든 점에 같은 투표 기회를 줌 → 투표가 이뤄진 누적 배열은 잡음이 많다.
위 그림의 경우 8-이웃을 사용한다면 색칠한 점이 극점이다.
극점만 남기더라도 잡음이 있어 보통 임곗값을 같이 적용한다.
그림에서는 비최대 억제로 점이 3개 남았는데 임곗값을로 설정하여 노란색으로 칠한 점 2개만 최종선택 되는 것.
#문제점 3#직선 방정식 y = ax+b 를 사용하면 기울기 a가 무한대인 경우 투표가 불가능하다.
==> 극좌표에서 직선의 방정식을 표현하는 식을 사용하여 해결
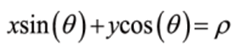
- 허프 변환은 직선의 방정식은 알려주는데 직선의 양 끝점은 알려주지 못함. 양 끝점을 알아내려면 비최대 억제 과정에서 극점을 형성한 화소를 찾아 가장 먼 곳에 있는 두 화소를 계산하는 추가적인 과정이 필요함.
- 허프 변환은 직선뿐 아니라 이론적으로는 어떠한 도형이라도 검출할 수 있는데 , 원의 경우 아래 방정식을 사용함. (a, b, r)의
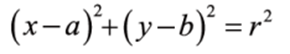
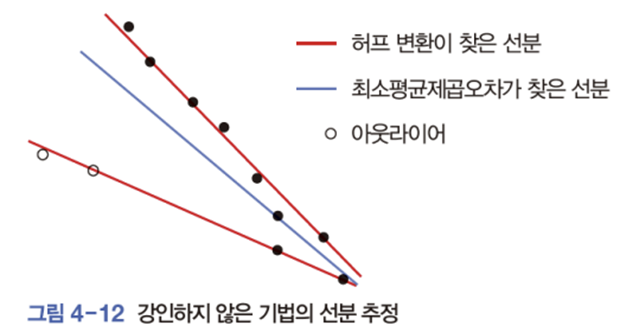
[아웃라이어가 섞여있는 상황]
- 허프변환을 이용하면 위 그림에서 빨간 직선 2개를 출력할 가능성이 높음.
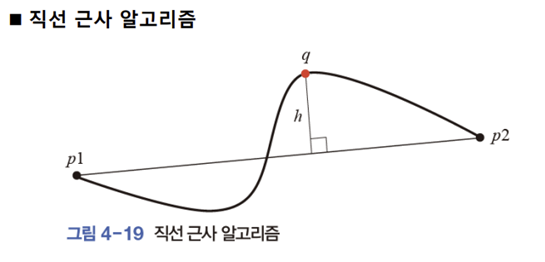
최소평균제곱오차 알고리즘 : 모든 점을 대상으로 오류를 계산하고 최소 오류를 범하는 직선 찾음.
- 아웃라이어의 영향으로 실제에서 벗어난 직선 찾는다
- 허프변환과 최소평균제곱오차 알고리즘 모두 아웃라이어에 민감한 강인하지 않은 기법.
- 인라이어와 아웃라이어 구별 없이 모든 샘플이 동등한 자격으로 오류 계산에 참여하기 때문에 아웃라이어의 영향을 크게 받을 수밖에 없다.
강인한 추정 : 아웃라이어를 걸러내는 과정을 가진 추정 기법
- 집단이 {1,1,1,1,16}일 때, 평균은 4로, 아웃라이어에 대처하는 능력이 전혀 없음. 중앙값은 아웃라이어를 배제하여 길이를 1이라고 추정하기에, 강인한 추정기법이라고 말할 수 있음.
- 중앙값을 사용하는 이유 : 센서노이즈에 의한 아웃라이어를 무시하기 위해
RANSAC : 인라이어와 아웃라이어가 섞여있는 상황에서 인라이어를 찾아 최적 근사하는 기법.
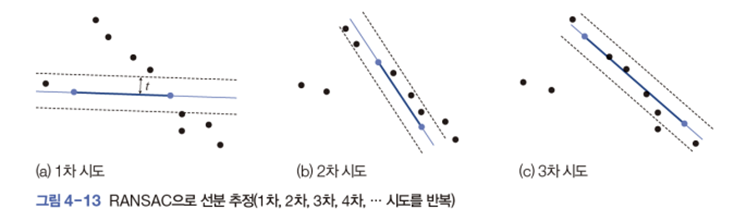
- 난수를 생성하여 추정하는 일을 충분히 많이 반복하고 가장 신뢰할 수 있는 값 선택
- 두 번째 시도는 임곗값 d(5)를 넘긴 7로, 점 7개를 가지고 최적 직선을 추정하고 추정 오류가 임곗값보다 작으면 후보군에 추가하고 그렇지 않으면 버린다.
- 난수를 사용하기에, 실행때마다 다른 결과 출력됨.
- 반복을 마치면 후보군에서 최적을 찾아 출력. 반복 횟수가 많을수록 진짜 직선을 찾을 가능성 높아짐.
but 소요시간 오래 걸림 - 랜덤 하게 두 점을 선택하고 두 점을 지나는 적선 계산. 일정한 양의 오차 t를 허용해 직선에 일치하는 점의 개수 센다. 개수가 임곗값 d를 넘지 못하면 가능성이 없다고 보고 버린다.
에지는 물체의 경계를 지정하기에, 에지가 완벽하다면 영역 분할 필요 없음
but 위 실험 결과에서 알 수 있듯이 명암 변화가 낮은 곳에서 뚫려 폐곡선을 형성하지 못하는 경우가 많음.
영역 분할 : 물체가 점유한 영역을 구분하는 작업
영역 분할 알고리즘 : 오츄 알고리즘 / 군집화 알고리즘 / 워터셰드 알고리즘

[워터셰드 알고리즘] : 비가 오면 오목한 곳에 웅덩이가 생기는 현상을 모방하는 연산
클러스트링( Clustering) 방식 : 데이터를 비슷한 특성을 가진 그룹으로 묶는 데이터 분석 기법
슈퍼 화소 : 화소보다 크지만 물체(전체 이미지) 보다 작은 자잘한 영역으로 과잉 분할
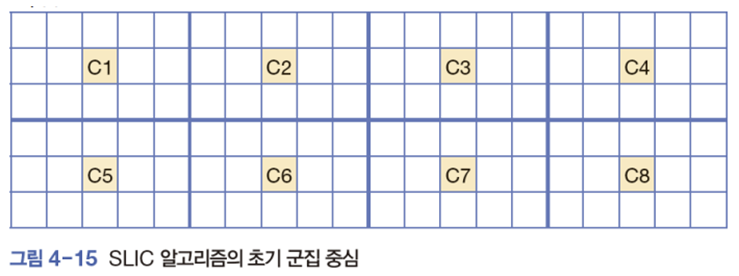
SLIC 알고리즘 : k-평균 군집화와 비슷하게 동작
- 각 군집의 중심값을 기준으로 요소가 어떤 중심값과 닮아있는지를 판별.
- 닮아있다 = 유사도 (s)

*D : 거리(d’pq)가 가질 수 있는 최댓값.
*d’pq : p포인트와 q포인트 사이의 거리 (얼마나 닮아있는지를 나타내는 지표)
→ 거리가 멀수록 유사도는 낮아짐. - 거리 :

*군집에 새로운 요소가 들어올 때마다 v’p와 v’q값이 바뀌기에 함숫값 이용
*f(v)는 v에 해당하는 화소의 색상(r, g, v)과 위치(x, y)를 결합한 5차원 벡터→ 포화될 때까지 계속 반복
탑 다운 방식 (top down) : 전체 시스템을 고차원적인 관점에서부터 살펴보고 시작하여 세부 사항을 처리하는 방식.
정규화 절단 알고리즘
- cut : 영상을 두 영역으로 분할했을 때 분할의 좋은 정도를 측정해 주는 목적 함수.
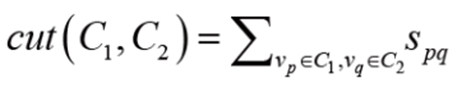
원래 영역을 2개의 영역 c1,c2로 분할했을 때 cut 식 - C1과 C2의 영역이 클수록 둘 사이에 에지가 많아 cut은 덩달아 커짐. -> cut 사용한 분할 알고리즘은 영역을 자잘하게 분할하는 경향.
- 두 영역C1, C2가 제대로 된 분할이라면 C1에 속한 v’p와 C2에 속한 v’q의 유사도 작아짐. (잘 분할이 되었다는 것 == 거리가 커야 함.)
- ncut : cut을 정규화하여 영역의 크기에 중립이 되게 해 줌

- ncut함수를 목적 함수로 사용하면 분할을 최적화 문제로 풀 수 있음.
- ncut이 작을수록 좋은 분할.
- 원래 영역 C에서 ncut이 최소인 분할 C1, C2을 찾아야 함. (방법은 몰라도 됨)
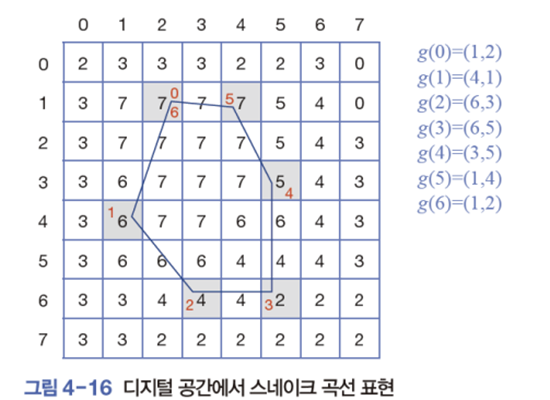
능동 외곽선 : 사용자가 물체 내부에 초기 곡선을 지정하면 곡선을 점점 확장하면서 물체 외곽선으로 접근하는 방법.
- 곡선이 꿈틀대며 에너지가 최소인 상태를 찾아가기 때문에 ‘스네이크’라고도 불림
- 매끄러운 곡선을 표현하기 위해 스프라인 곡선 g(l)을 이용.
- 2차원 상의 스프라이트 곡선은 g(l) = (y(l), x(l))로 표현.
- 매개변수 l은 [0,1] 범위의 실수인데 폐곡선을 이루기 위해 g(0)=g(1)이다.
- 디지털 영상은 이산 공간이기 때문에 l을 0,1,2,..., n으로 표현함.
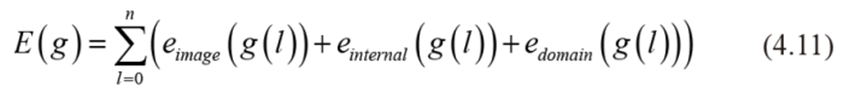
: 스네이크 곡선 g의 에너지 E = 영상 에너지 e’image, 내부 에너지 e’internal, 도메인 에너지 e’domain의 합.
- 영상에너지 e’image : 물체의 경계에 에지가 나타난다는 사실에 기반하여 곡선이 에지에 위치하도록 유도. (실제 구현에서는 에지 강도 사용)
- 내부 에너지 e’internal : 곡선이 매끄러운 모양이 되도록 유도. 일반적으로 물체의 경계는 급격하게 꺾이는 곳보다 매끄럽게 변하는 곳이 더 많다는 사실에 기반. (실제 구현에서는 곡률 사용)
- 도메인 에너지 e’domain : 분할하려는 특정 물체의 모양 정보를 더 잘 유지하도록 유도.
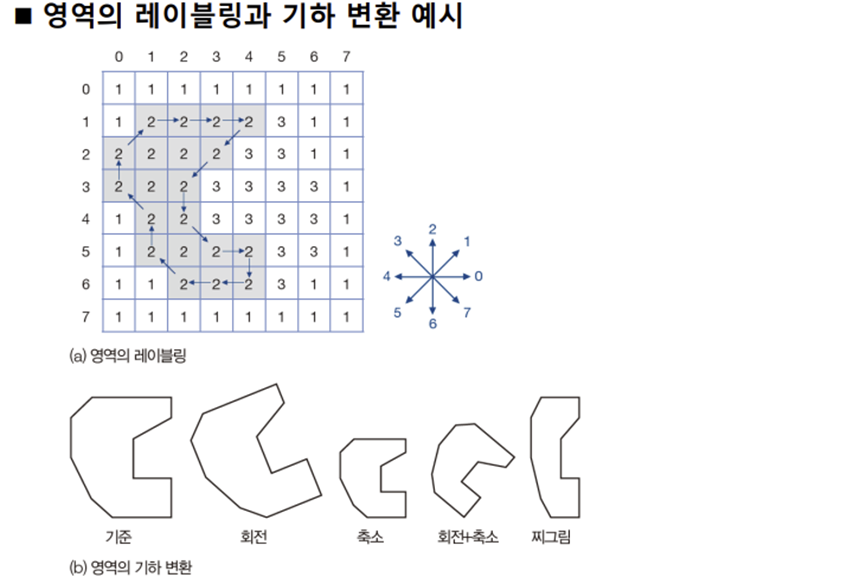
물체는 다양한 변환을 거쳐 영상에 나타날 수 있다.
불변성 : 변환을 해도 특징의 값이 변하지 않는 것. <-> 등변성

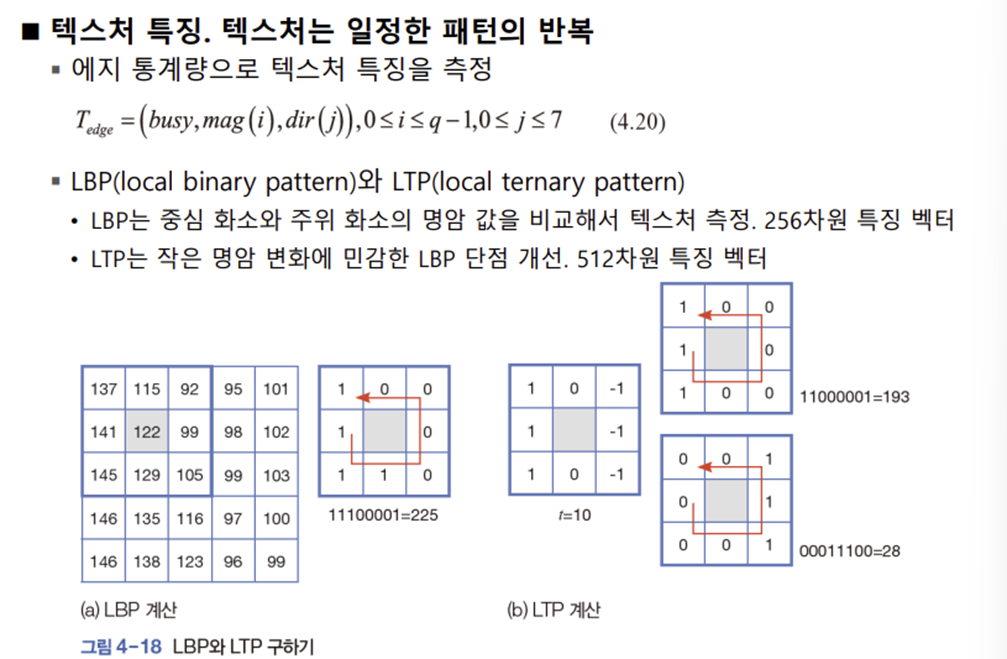
- LTP가 노이즈에 덜 민감함
'Electronic Engeneering > Intelligent System' 카테고리의 다른 글
| [지능시스템] 03장. 영상 처리 (2) | 2024.08.29 |
|---|---|
| 마우스 클릭을 통한 실시간 전경 표시와 GrabCut 알고리즘 코드 분석 (1) | 2024.08.27 |
| [지능시스템] 08장. 컨볼루션 신경망 (0) | 2024.08.27 |
| [지능시스템] 07장. 비전 에이전트 (0) | 2024.08.27 |
| [지능시스템] 06장. 비전 에이전트 (0) | 2024.08.26 |